Topology studies properties of spaces that are invariant under any continuous deformation. It is sometimes called “rubber-sheet geometry” because the objects can be stretched and contracted like rubber, but cannot be broken.

• What is Topology
  • 重要的拓扑性质
  • 定义
    • 欧式空间中的开集
    • 距离空间 -> 拓扑空间
• 同胚映射 Homeomorphism
  • 同胚

What is Topology

研究几何图形或空间在连续改变形状后还能保持不变的一些性质。只考虑物体间的位置关系，而不考虑其形状和大小

主要讨论点集拓扑学

重要的拓扑性质

• 连通性
• 紧致性

定义

存在集合$X$，其全部子集的集合叫做$X$的幂集，记作$2^X$。集合$X$的拓扑$\tau\in 2^X$，且满足下面3个性质

1. $X\in \tau, \emptyset\in \tau$
2. $\tau$中有限个集合的交集属于$\tau$
3. $\tau$中任意多个集合的并集属于$\tau$

将满足这些性质的集合$\tau$中的元素叫做开集，集合$\tau$即$X$的拓扑

欧式空间中的开集

• 设$U\subseteq \mathbb{R}^{n}$为欧式空间的子集。若$\forall x\in U, \exists r>0$，使得球形邻域$B(x, r)\subseteq U$，那么$U$就叫开集
• $U$是开集当且仅当对于$\forall x\in U$，总能找到某个球形邻域$B(x, r)\subseteq U$

距离空间 -> 拓扑空间

• 设$(X, d)$为距离空间，其开集族为$\tau_{d}$，可证其满足上述3条性质；从而$(X, \tau_{d})$成为拓扑空间，其拓扑$\tau_{d}$称为由距离$d$诱导/生成的拓扑
• 设$(X, \tau)$为拓扑空间，若存在$X$上的距离函数$d$，使得距离诱导的拓扑$O_{d}=\tau$，就称$X$可距离化

同胚映射 Homeomorphism

设两个拓扑空间$(X, \tau_{X}), (Y, \tau_{Y})$，并且使$f: (X, \tau_{X})\rightarrow (Y, \tau_{Y})$。$f$被称为这两个空间之间的同胚映射，当且仅当

• $f$是一个双射
• $f$是连续的
• $f^{-1}$是连续的

同胚

称两个拓扑空间$(X, \tau_{X}), (Y, \tau_{Y})$是同胚的/拓扑同构的，记作$X\cong Y$，当且仅当这两个空间之间存在一个同胚映射$f$

• 同胚是一个等价关系
• 在欧式度量空间中，任何开区间都是同胚的。例如，该空间中的开区间$(0, 1)$与$(1, \infty)$就是同胚的，有同胚映射

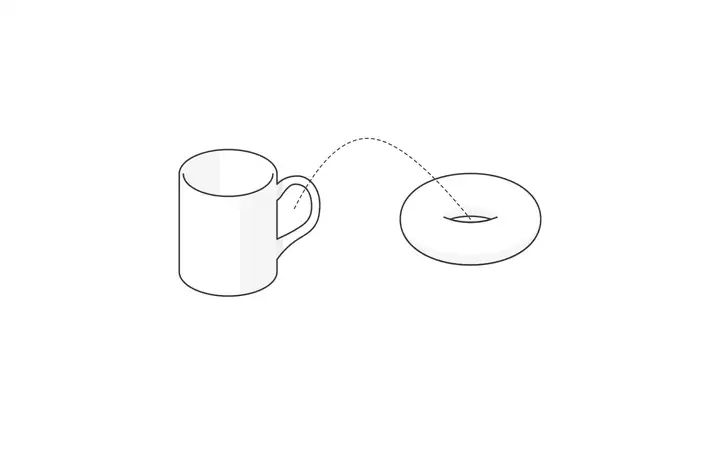
• 两个空间是否同胚，可以被看作一个空间是否可以形变为另一个空间的可能性。直观条件：如果一个空间是有洞的，那么它通过一个同胚映射称为另一个空间之后，这个洞依然是保留的